Yes, but what time is it?
The first part of this story was about how the Sun goes across the sky, from morning to night: from east to west, which means that the shadows on a sundial move from left to right. It was also about how the Sun goes up and down the sky, between the 21st of December and the 21st of June: it is in the south in December, in the north in June, so that the shadows are nearer the top of the picture in December and nearer the bottom in June. (The lines look darker at the edges because they are close together in December and June, when the Sun hardly moves up or down at all).
 December to June at Greenwich
December to June at GreenwichAfter that, it was a matter of geography. At Greenwich, in the Northern Hemisphere, the winter shadows are further away from the centre of the sundial and the summer ones are closer to it, swooping downwards at a steep angle on either side. At Reyjkavik, further north, the summer shadows get steeper and closer together as if they were trying to join together, and at Thule, in the Arctic Circle, some of do join together, to make ovals, meaning that for some days in the middle of summer the Sun never sets but just goes round and round. Finally, at the North Pole, the Sun doesn't set for half the year, and the shadows are circular (or rather, one very long spiral).
This was interesting and the pictures were beautiful, but the sundial wasn’t telling us the one thing sundials are meant to do best: indeed, the reason they exist in the first place. It wasn’t telling us the time.
A perfectly logical sundial
Thinking through it, it is fairly easy to see how a sundial ought to work as a timepiece. At 12 noon the Sun is in the south and its shadow is at the top. At 12 midnight the Sun is in the north and its shadow is at the bottom (you’d need to be in the Arctic Circle to see the sun at that moment, but if you did see it, that is where it would be). So, logically, 6pm will be half way between top and bottom, sticking out to the right, and 6am will be half way as well, sticking out to the left.
The unfortunate truth
None of this is true. A logical sundial can’t tell the time.
Here is what the hours really look like. (I have removed most of the daily shadow lines to make the picture clearer). The thick red line in the middle shows the shadow of the Sun at 12pm each day.
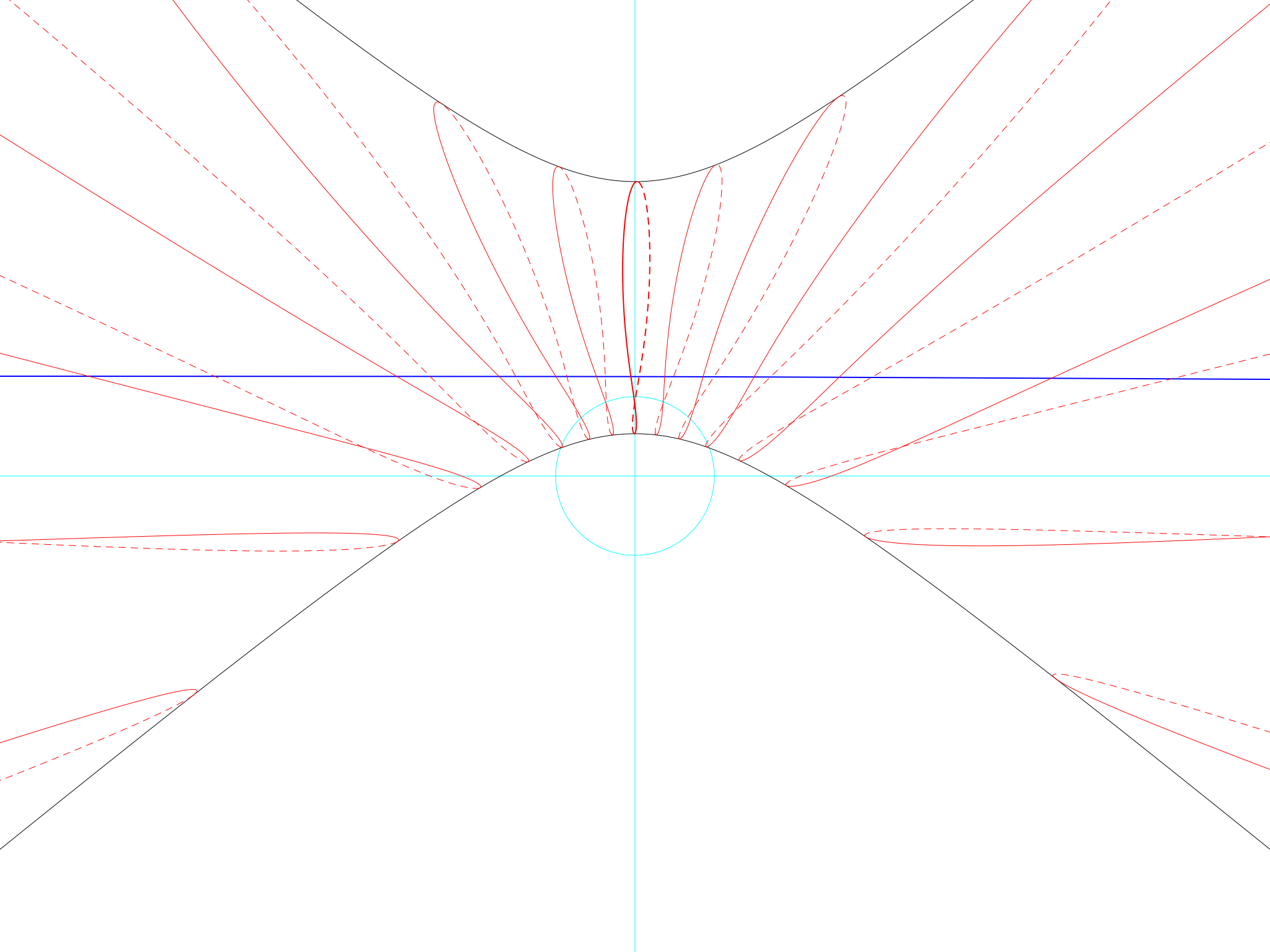 Hour lines at Greenwich
Hour lines at Greenwich
The line is not a line, but a twisted loop. It starts at the top in December, comes down the left-hand side in January, February and March, and then shortly before June comes along it crosses over and comes down on the right instead. From June to December the journey is reversed: I have indicated it by a dotted line.
All the other hours are there: 11am (and earlier) to the left of 12pm, 1pm (and later) to the right.
Near the top, the dotted line for 12pm gets quite close to the solid line for 1pm. If you look at a sundial when the shadow is in that sort of area, you won’t be able to say “It’s 12.30”, only “Either it’s a little after 12pm in February or it’s a little before 1pm in November”. If you happen to know the date, then you will know the time, but that still doesn’t seem right. Something as fundamental as a sundial ought to be able to tell the time without help!
Something is crooked in the cosmos.
Frustration and delight
Astronomy is made out of layers of delight and frustration. This is what makes it worth doing at all: a discipline that got everything right first time would not be worth the bother. There is delight at discovering that nature is regular; frustration at discovering that the regularity isn’t regular; further delight when you discover that the irregularities have a pattern to them: that they are (in their own way) regular.
To take one example: the ancient astronomers observed the stars we see every night and saw that they were fixed relative to one another. Each night, they rose and set in the same pattern and in the same order.
So, naturally, the astronomers made maps of the stars and measured the position of each one as exactly as they could, an achievement that was to stand for all time.
The astronomer Hipparchus, working in the late 2nd century B.C, found that his predecessors working a century before had got the positions of the stars wrong by a moderately large amount, in some cases as much as twice the width of the full moon. The old-school astronomers seemed disappointingly slapdash in their measuring – until Hipparchus discovered that the error in a star’s measured position depended on where it was in the sky. There was a pattern to it.
It turned out that the Earth’s axis is not fixed in space, pointing towards Polaris, the Pole Star, as most of us remember from school. It follows a huge circle in the sky, moving rather less than a degree (two Moon-widths) every century and taking 26,000 years to complete its circle. This movement is called precession.
Suddenly the old astronomers’ errors were not errors, but data, and the data had yielded a new and unexpected result.
To add to the delight, the records of Babylonian astronomers of 500 years before, which had seemed too inaccurate to be any use, turned out (when corrected for precession) to be accurate after all, and invaluable for the study and precision of eclipses.
The egalitarian science
Astronomy is practically unique among the sciences. Think of another science, such as chemistry. Chemistry is about the elements, their reactions, and the compounds they create. Sodium (a soft shiny metal) and chlorine (a toxic pale green gas) make sodium chloride, table salt, which is not shiny, or green, or poisonous. Calcium (a soft greyish metal), carbon (deep black) and oxygen make calcium carbonate: chalk, the rock that hills are made out of. There is nothing black about chalk. Calcium and oxygen and sulphur (bright yellow) make calcium sulphate: gypsum, the kind of chalk that is used on blackboards. As we all know, it isn’t yellow.
These facts are certainly part of the charm of chemistry, but how do I know them? I know them (or rather, believe in them) because I read it somewhere or because a teacher told me – told me, because he had read it somewhere. And the writer of the book wrote what he wrote because he, in turn, had read it somewhere.
Chemistry is built on tradition and authority and the most we can ever do, if we are lucky, is confirm little bits of it by our own experiments.
If we are allowed to, that is. The trend of science education is all against discovery and all in favour of learning the teachings of our ancestors and uncritically believing in them. The only purpose of an experiment is to demonstrate the truth of something we already know is true. If the facts don’t match the theory then the facts must be wrong.
When the writer Richard Holmes grew an enormous crystal of copper sulphate and presented it triumphantly to his teacher, expecting praise, the teacher wouldn’t even look at it. It was too big; it was obviously a fraud made of blue glass. If the teacher had touched the crystal with a damp finger and then sucked the finger, he would have tasted the unmistakable metallic taste of copper; but did he? Of course not, because he already knew it was a fake.
When I found by experiment that throwing salt into an almost-boiling saucepan would often get the water to boil, my own science teacher knew at once that it was impossible because salt water boils at a higher temperature than fresh. He refused to discuss the matter: better to dismiss the phenomenon than waste time trying to find an explanation for it. (My guess is that the sharp edges of the salt crystals made nuclei on which bubbles of steam could grow).
The data above my head
The great thing about astronomy is that it is not chemistry. I don’t need to sign up to an entire system of belief before I can talk about it (the existence of atoms, the way molecules are made, and so on). The raw data of astronomy are there for anyone to see, experts and laymen, the ancients and the moderns alike.
If I want to see for myself the data Hipparchus was working with, I go out into a dark field on a clear night, and I look up. I can think like him, and check his work.
That is all. I don’t need anyone to tell me what I am seeing.
If I want to measure the circumference of the Earth the way Eratosthenes of Alexandria did, I don’t even need a dark field. I just set up a stick at noon, measure its shadow, and get a friend a hundred miles away to do the same.
The raw materials of chemistry – the elements – are discovered by specialised equipment and confirmed by books and tradition. The raw materials of astronomy – the movements of the sun, moon and stars – are open to each of us. They are in front of our noses (or above them). The only equipment we need to do fundamental astronomy is our eyes and our brains.
The relativity of time
A politician is someone who, when you ask him what the time is, asks you what time you would like it to be. This is a joke about politicians but it is a fact about science.
The movements of the Sun through the sky are a smooth, continuous process. It makes sense to chop the movement into equal pieces and call each piece an hour.
The ticking of a clock, or the burning of a candle, or the dripping of a tap – even the roasting of a joint of meat – are regular processes. It makes sense to measure their progress and call so many ticks, so many drips, so much wax burnt, an hour.
That has given us two different meanings of “hour”. What the sundial has told us, with its loops instead of lines, is that the two kinds of “hours” are different things.
The Romans (and civilised people everywhere, for many centuries afterwards) used to divide the day, from sunrise to sunset, into twelve equal parts. The hour after sunrise was the first hour, and the 12th hour was the hour before sunset. You can see this still in the Gospels: “the ninth hour” means “the middle of the afternoon”.
You might say that the trouble with Roman hours is that they are different lengths at different times of year, but you are jumping the gun here, because without a standard of length, how can you tell what is long and what is short? All we can say for certain is that a joint of meat that needed cooking for one Roman hour in summer (when the days are long) would be half raw if you cooked it for one Roman hour in winter, when the days are half the length.
On the other hand, if you preferred sundials to roast beef, you could just as well say that the trouble with a clock hour is that it covers a different amount of the daytime in summer and in winter, and you could point out that a sundial calibrated in Roman hours is entirely made out of straight lines, like this:
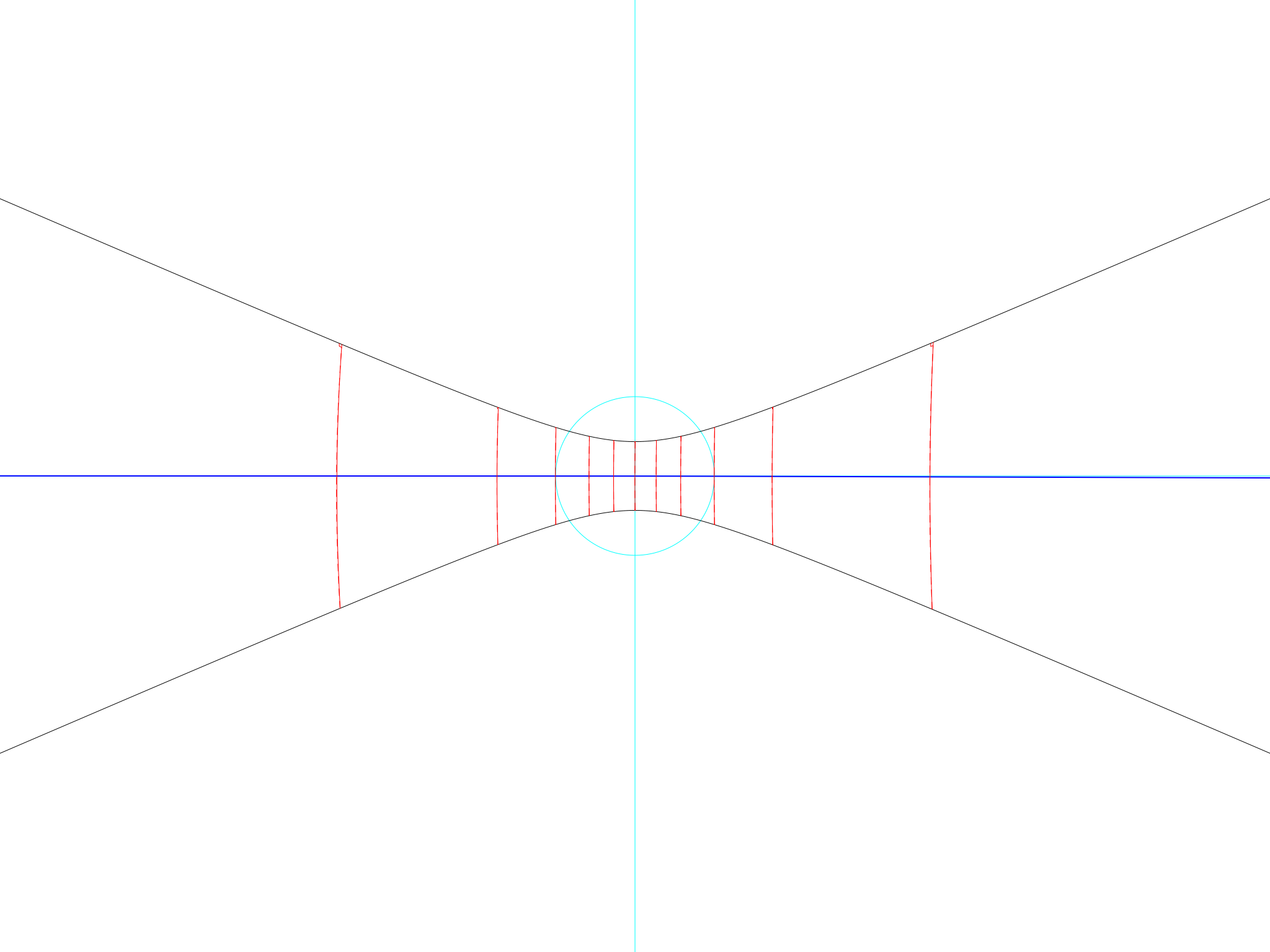 Roman hours at the equator
Roman hours at the equator
In the end, it is clock hours that have won the battle, because all physical processes, from cooking to the vibrations of atoms, go at the same pace at each other. It makes much more sense to use them as the definition of hours, minutes and seconds, and to admit that the movement of the sun in the sky is irregular. But I wanted to mention the battle all the same, because it is important (now and then) to remember that the definition of time is not given to us from outside: it is a deliberate choice.
Changing definitions
An hour used to be one twenty-fourth of the average period between one noon and the next. Then atomic clocks came in, and scientists changed the definition. Now an hour is “the duration of 33,093,474,372,000 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium-133 atom at a temperature of 0°K”.
This doesn’t change how long the hour actually is, but it reflects our belief that, in the grand scheme of things, the way atoms vibrate is more fundamental than the way our planet happens to be spinning at the moment. If, one day, the exchange rate between “atomic hours” and “Earth spin hours” happens to change, we will find it easier to believe that the Earth has changed speed than to believe that atoms of caesium have decided to behave differently.
(And indeed, largely because of the Moon and the tides, the Earth’s rotation is getting slower and an Earth hour is getting longer than an atomic hour. Every few years a “leap second” is added to atomic time to keep it in step with the Earth.)
Time in Japan
Most of the world discovered clocks after they had discovered the merits of what I’ve called “clock hours”. The Japanese didn’t. When that nasty but convenient foreign invention, the clock, arrived in Japan, it arrived in a country which still counted twelve hours from sunrise to sunset and wasn’t about to change its civilised habits because of some new-fangled barbarian contraption.
So early Japanese clocks work according to clock time (they can’t do anything else) but they indicate civilised sunrise-to-sunset time. I have seen some of them. They have movable markers to indicate when each civilised hour comes along. Since the length of a civilised hour relative to a clock hour varies with the time of year, a caste of itinerant astronomers arose. An astronomer would visit you every few weeks to adjust your clock, just like a piano tuner coming to tune your piano.
The relativity of movement
The definition of the hour is just one example of an important principle in astronomy. Astronomical judgements are relative. Does the Earth rotate under a stationary sky or does the sky rotate above a stationary Earth? These are not questions of fact, they are decisions. Whichever answer you choose, you can build a completely consistent theory which fits all the known data. The reason for choosing one answer rather than another is if one answer makes better explanations than the other, and simpler physical laws.
For the Earth, the Sun and the stars, here are the main options:
- Stationary Earth: The Earth stands still. The Sun orbits it once every 24 hours, in a stange spiral pattern that reaches 23½°N in June and 23½°S in December. Quite separately from this, the fixed stars also orbit the Earth, once in about every 23 hours and 56 minutes.
- Earth spinning every 24 hours: The Earth rotates beneath the Sun and stars. It makes one revolution every 24 hours. The Sun bounces up and down between 23½°N and 23½°S and also waggles from side to side in a rather odd loop. As for the stars, these revolve very slowly from west to east. They move a little less than a degree a night, making one revolution per year.
- Earth spinning every 23 hours 56 minutes: The Earth rotates beneath the Sun and stars. It makes one revolution every 23 hours 56 minutes. The stars are stationary. The Sun orbits the Earth from east to west, following a slanting path among the stars: this is called the ecliptic. It moves about one degree a night, making one complete orbit each year.
- Earth spinning and orbiting: The Earth orbits the Sun once a year. In addition, it rotates on its axis once every 23 hours 56 minutes. The stars are stationary. The Earth’s axis is tilted, relative to its orbit, at an angle of 23½ degrees.
Which description is right? All of them are.
“Stationary Earth” sounds prehistoric. But all of us use it every day when we talk about the Sun rising and setting. We don’t seriously talk about “the Earth carrying us into view of the Sun” in the morning, or getting in the way of it in the evening.
“Earth spinning every 24 hours” is another picture we use every day. Down here, we live our lives by it. But if we look up at the sky then it feels wrong because of the Sun bouncing north and south and waggling east and west, as shown by those ugly loops on the sundial.
“Spinning every 23 hours 56 minutes” is the most natural way of looking at things when we want to think carefully about celestial motions. It is convenient for calculation because nothing moves in more than one way. The Earth spins, but that is all; and the Sun orbits, but that is all. This is the description that was used for millennia and it let us predict eclipses and the exact positions of the planets in the sky.
“Spinning and orbiting” is the way Galileo insisted we should think. He did without actual proof, because as far as astronomy without high-precision telescopes is concerned there is no difference between this description and the last one. The first time one could really speak of “spinning and orbiting” being proved was in 1838, when Friedrich Wilhelm Bessel found that the position of the star known as 61 Cygni every March was one five-thousandth of a degree west of its position each September. Even then, you could stick to a stationary Earth if you wanted to, but you would then have to say that a distant star was dancing round itself once every twelve Earth months, which sounds unreasonable. It makes much more sense to say that the shift comes from a change of perspective as the Earth orbits the Sun. So that is what we choose to say. As a bonus, it leads to the conclusion that the distance of 61 Cygni must be about half a million times the distance between the Earth and the Sun. This was the first time anyone had ever measured the distance to a star.
As for the story I am telling here, because all these descriptions add up to the same thing in the end, and any of them can be translated into any of the others, I’ll use whichever one happens to seem convenient at the time.
Why 24 hours?
Let’s start with the simplest picture of all: the one where the Earth does not spin at all.
Lie outside on a clear night, on your back on the stationary Earth, and look up. You will see the stars wheeling over you as the hours pass. They wheel from east to west. Whenever some stars set in the west, new ones will rise in the east.
If you do the same again the next night, and the one after, it will look much the same; but if you check your watch each time, you will notice a subtle difference. Each night, any given star rises or sets four minutes earlier than it did the night before. At least, that is what conventional watch-users will say.
At this point you have to take the first imaginative step, which is to discard your watch and your 24-hour ideas and let the stars be your clock. A sidereal day or “star day” is the period from any given star being in a certain position in the sky to it being in the same position again the following night: from “star-rise” to “star-rise”, if you like. A sidereal day is 23 hours, 56 minutes and 4.0916 seconds.
Once you have made the change, you can put your watch away because the stars above you are themselves a huge clock. They complete precisely one revolution every sidereal day. Measured according to the star clock, the stars don’t rise or set at different times each night: any given star always rises or sets at exactly the same time. That isn’t an extra fact about stars – it’s simply what sidereal time means.
There is one more thing you will notice when you look up at the stars night after night. All the stars are fixed relative to one another, in patterns we call constellations – except for seven of them. Those seven wandering stars move across the sky. Five of those wanderers are called ‘planets’ (the word means ‘wanderer’ in Greek): they are Mercury, Venus, Mars, Jupiter and Saturn. The sixth wanderer we call ‘the Moon’. The seventh wanderer is the Sun. The Sun is so bright that when it is in the sky, the sky itself turns from black to blue and all the other stars disappear.
The Sun moves along an invisible line in the starry sky, which is called the ecliptic. (All the other wanderers move near the ecliptic in a broad path called the zodiac, but we don’t need to think about them now).
The movement of the Sun is simple, slow and steady. The Sun moves from west to east among the fixed stars by about a degree a day, until after 366¼ star-days it comes back to where it started. We call this period of time “a year”’. In the course of a year the stars have made 366¼ revolutions around the Earth, east to west, but the Sun has made one revolution backwards (west to east) relative to them. 366¼ forwards minus 1 backwards equals 365¼. And indeed, when we aren’t thinking about the stars, we know that there are 365¼ [solar] days in a year.
All this has been known since ancient times.
It is possible to use the Sun as a calendar by looking at where it is relative to the fixed stars. For instance, when the ancient Egyptians saw the Sun rise shortly after the bright star Sirius, they knew that the Nile was about to flood.
Now let’s change our point of view one more time. So far, the stars have been spinning above you, once every sidereal day, and the Earth has been standing still. Now stop the stars, and set the Earth spinning instead.
Nothing has changed except the description. The Earth is now revolving from west to east every 23 hours 56 minutes, underneath the fixed, unmoving stars. The stars appear to rise in the east as the Earth, revolving eastwards, carries you into sight of them, and to set in the west as the Earth, revolving away from the west, carries you out of their sight.
Just as before, the Sun moves along the ecliptic relative to the stars. Just as before, it travels from west to east, 1/366.25 of a revolution each star-day. (That is about 0.983 degrees).
Now that we have this description, lie on the ground at noon and look up at the Sun. Memorise where you are looking, then shut your eyes. Keep them shut for 23 hours 56 minutes, a whole sidereal day. The Earth will turn underneath the stars, west to east, and you will turn with it, until you have come all the way round and you are back where you were.
Open your eyes. You are facing towards the identical portion of sky, towards the identical star (though you will not see it because the sky is bright). But the Sun is not there any more.
While you had your eyes shut, the Sun has moved eastwards by 1/366.25 of a full revolution. That is, it is now 0.983° east of where you are looking. But there is no need to worry, because the Sun is not lost. The Earth is turning from west to east, so all you need to do is wait a little bit, for the turning Earth to take you eastwards to where the Sun is now.
That extra bit of turning to catch up with the moving Sun takes just under 4 minutes. Added to a star-day of 23 hours 56 minutes, that makes a full sun-day of 24 hours.
And that is why we say that the day is 24 hours long.
The Equation of Time
I have just gone into a lot of detail to show why the day (measured from one noon to the next) is 24 hours long. But in fact we know that it isn’t 24 hours long. The sundial proves that, because if the day had been exactly 24 hours long always, the hour lines on the sundial would have been straight, without any loops in them. The hour lines aren’t straight and do have loops in them, so the day can’t always be exactly 24 hours long after all.
The difference between sundial time and clock time is called the Equation of Time. It varies throughout the year. The time from one noon to the next can be anywhere between 20 seconds shorter and 20 seconds longer than 24 hours. This doesn’t sound much, but if it carries on like that for day after day, it all adds up. At the extremes, a sundial can be about a quarter of an hour faster or slower than a clock.
What was missing in my 24-hour explanation? I made two assumptions. I assumed that the Earth always turns at the same speed, and that the Sun always travels east at the same speed. The first assumption is correct, but the second isn’t. It is wrong for two reasons.
The obliquity of the ecliptic
The Sun does not travel along the equator. It travels along the ecliptic, which is tilted relative to the equator, at an angle of 23½°.
At the summer solstice, on 21 June, when the Sun is in the constellation Gemini, it is 23½ degrees north of the equator; at the winter solstice, on 21 December, when the Sun is in Sagittarius, it is 23½° south.
This is called ‘the obliquity of the ecliptic’ and it is why we have the seasons. Summer in the northern hemisphere is when the Sun is north of the equator and winter is when it is south.
If you want to understand the reason why the ecliptic is tilted, think of the Earth orbiting the Sun, with the Earth’s axis of rotation not upright relative to its orbit, as you might expect, but with the North Pole tilted 23½° towards Gemini. The direction stays the same as the Earth goes round the Sun, so that half a year later, when the Earth is on the other side, the North Pole is still pointing towards Gemini, but now the Sun is in the other half of the sky; so that pointing towards Gemini means that the North Pole is pointing away from the Sun.
The effect of the obliquity
This is embarrassing. When I started thinking about the variable length of the day, I very quickly worked out that the eccentricity of the orbit comes into it (I’ll describe that effect later). I was so pleased with myself that when the idea came up that the tilt of the Earth’s axis might have something to do with the length of the day as well, I didn’t even consider it. I had found a solution (this is true) and I thought that my solution was the whole of the answer (this is not true).
I thought that the fact that the ecliptic is tilted at 23½° makes no difference to the distance that the Sun travels east each day. I was wrong.
Here is what I should have thought, right from the beginning. If I had told myself this story then I would have convinced myself that the ecliptic mattered and was worth thinking about.
There are three things that are always worth doing when trying to handle new ideas (as opposed to learning things from books):
- Take an extreme case because then the effects will be more noticeable.
- Picture what is going on.
- Don’t calculate.
(Einstein was a firm believer in “Think about the picture first, don’t calculate till later”.)
So: 23½° isn’t a very steep angle. So let’s try an angle that is very nearly 90° but not quite. (I wanted to avoid having it 90° exactly, because that would take it exactly through the North Pole, which might make the motion a different kind of thing).
The question I am asking when trying to understand the obliquity of the ecliptic is “When something goes eastwards along a path that is inclined to the equator, and goes at a steady speed, does it always go eastwards at the same rate?”
So let’s forget about the Sun, because it is up in the sky and we don’t have many instincts about it. Let us stay on the surface of the Earth instead, and let’s imagine that I am travelling across it at a very steep angle. To make it seem more natural, I will go slower than the Sun. I will travelling at 60 nautical miles per day, which is a convenient number for story-telling because the definition of a nautical mile says that 60 nautical miles equal one degree.
If I were to travel straight along the equator, then I would travel 60 miles a day and I am 1° further east each day. So in that case, yes, my eastward motion would be steady and unchanging.
But I am not travelling along the equator but along a route tilted very nearly 90° relative to it. In that case I will still travel 60 nautical miles on my first day, but it’s very nearly directly northwards; so my first day’s travel takes me 60 nautical miles north and only a few inches east. My eastward movement, my change of longitude, is not more than a thousandth of a degree a day.
So – result 1 – near the equator (which for the Sun, would be at the equinox), my eastward speed in longitude is less than my walking speed.
Nothing much happens for the next few weeks. After just over 7 weeks I get to Greenwich. I am a yard or so to the east of the Greenwich meridian by then. Still I am going essentially northwards, and still my eastward speed is a tiny fraction of a degree per day.
Finally, after almost three months, I get to the North Pole. Because of that slight eastward drift, I am not travelling directly towards it, but a little off to one side. The North Pole is ahead of me but several feet to the left of my path.
That means that as I walk past the North Pole, it moves, in a very few paces, from being in front of me, to being directly to my left, to being behind me. In those few paces, although I haven’t changed direction, my direction of travel as measured by the Earth has changed from northward to eastward to southward. And in those same few paces my longitude has changed from almost 0° east to 90° east to 180° east, as my journey turns into a journey south towards the South Pole.
So – result 2 – far from the equator (which, for the Sun, would be at the solstice), my eastward speed in longitude is more than my walking speed.
There is a bonus result which I should mention. Remember that even at Greenwich my direction was mostly north with only a tiny bit of east in it.
Result 3: half way between, my eastward speed in longitude is not the same as my walking speed. It is less.
I got all this simply by making pictures in the head, without any calculation at all. The pictures are easier to visualise if you look at a globe and see how the lines of longitude get closer together as you move away from the equator; but even without a globe, the imagination is not over-stretched. You could do it in the shower.
Armed with these results, it is easier to go back to the real ecliptic, tilted at an angle of 23½°, and make some real calculations – easier because now we know that the calculations are worth making, and which calculations they are. So here goes:
- When the ecliptic crosses the equator, at the equinoxes, the Sun is moving along the ecliptic at a steady speed of 0.983° per day. Because of the obliquity of the ecliptic, this means that it is travelling eastwards at 0.983 × cos(23½°) = 0.901° per day: eight hundredths of a degree slower. Because the Sun is slower, the Earth needs to turn a little less before it catches up with it at the end of the day: eight hundredths of a degree less, which saves about 20 seconds of time.
- When the ecliptic is as far as it can be from the equator, at the solstices, the Sun is moving along the ecliptic at a steady speed of 0.983° per day. Because it is not at the equator but 23½° north (or south) of it, this means that the Sun is travelling eastwards at 0.983 ÷ cos(23½°) = 1.072° per day: nine hundredths of a degree faster. So the Earth needs to turn a little more before it catches up with the Sun at the end of the day: nine hundredths of a degree less, which takes an extra 21 seconds of time.
So the obliquity of the ecliptic means that the noon-to-noon ‘day’ is 21 seconds longer than 24 hours in December and June and 20 seconds shorter than 24 hours in March and September. Twenty-odd seconds don’t sound like much, but they add up, day after day. At worst, the accumulated difference between clock time and sun time can add up to almost 10 minutes.
(Why did I want to point out the bonus result about what happens half way? Because many published descriptions of the Equation of Time say that the effect of the obliquity is “a sine wave”, meaning that it is exactly symmetrical and therefore will be zero when we are half way between a solstice and an equinox. Now, without any calculation at all, I have proved them wrong. Mathematicians love not having to calculate things.)
The 10-minute variation is a big one and it makes a big difference on the sundial.
Here is how the hour markings on a sundial would look if the obliquity of the ecliptic were the only difference between mean time and real life:
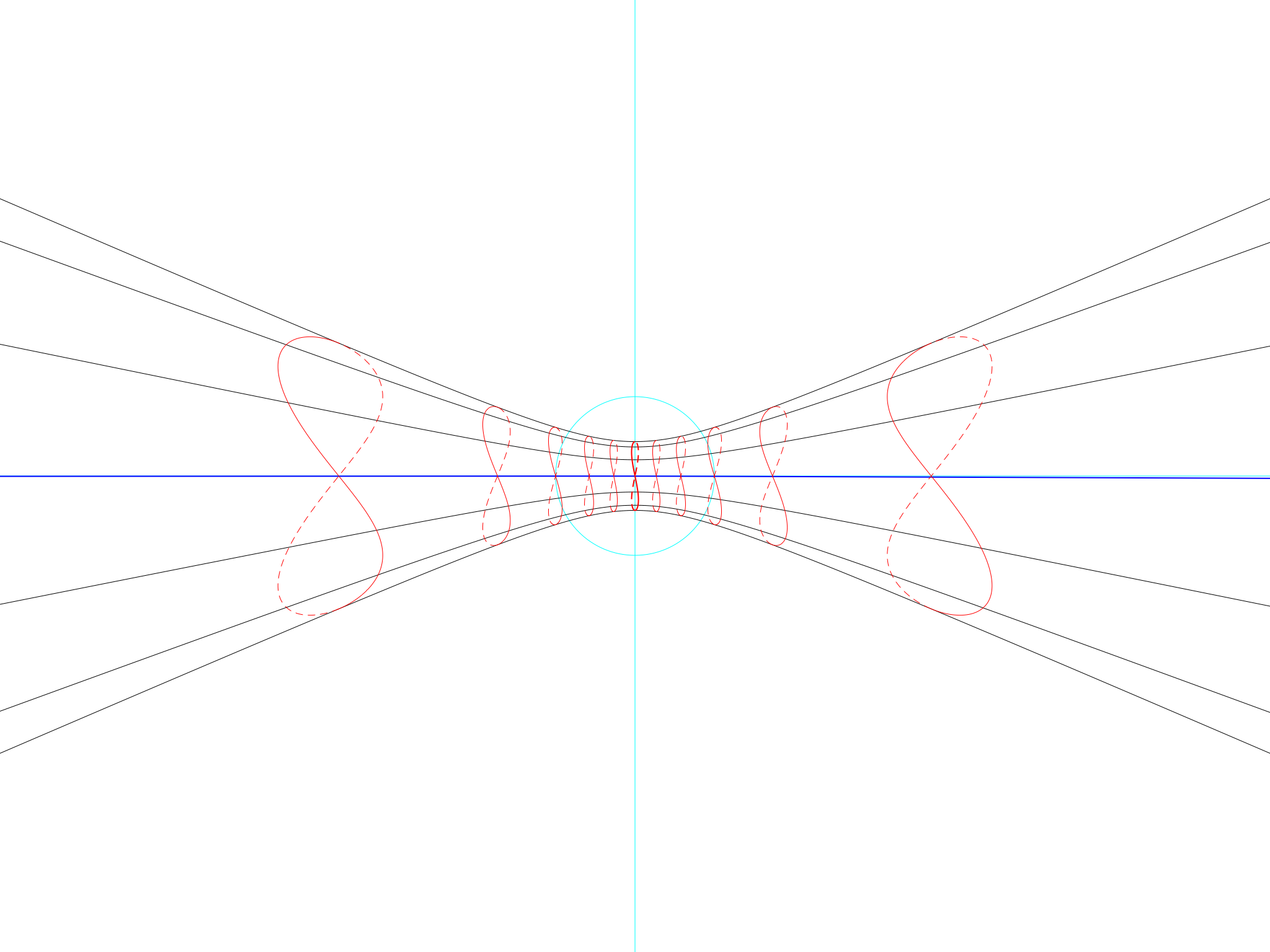 Hour lines at the equator (obliquity only)
Hour lines at the equator (obliquity only)
We have got somewhere, but we aren’t quite there yet, because these loops are elegant and [very nearly] symmetrical. The loops on a real sundial are asymmetrical and bulgy. To remind you, they look like this:
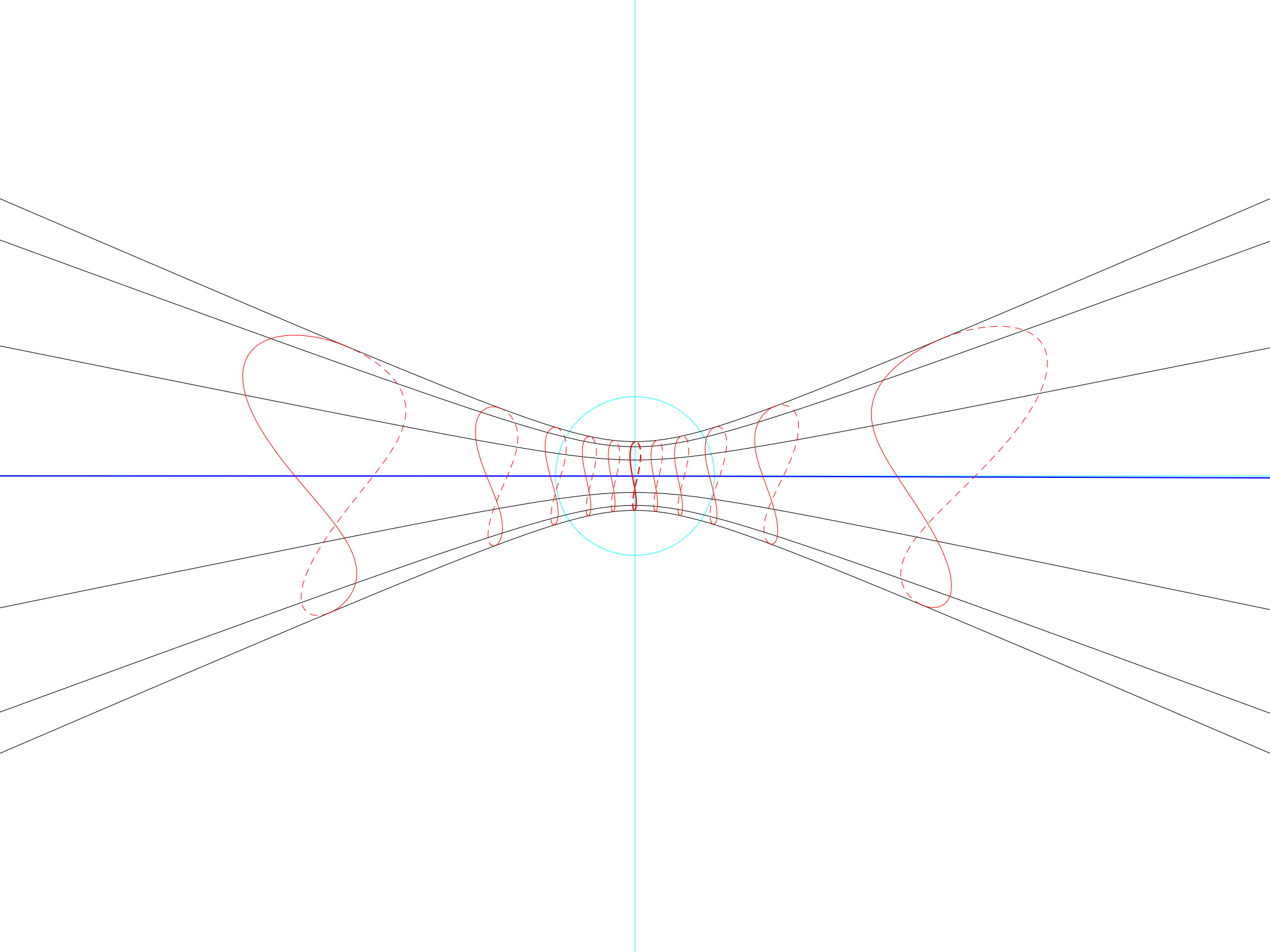 Hour lines at the equator (real orbit)
Hour lines at the equator (real orbit)
So there is more work to do.
On other planets
What the hour lines look like on different planets depends on how much their axes of rotation are tilted relative to their orbits.
Pluto’s axis is tilted a whole 119½° away from the upright. This effectively means that it spins upside down. Completely upside down would be a tilt of 180°, so Pluto’s axis is 60½° away from perfect upside-downness.
If you lie on your back on Pluto you will see the ecliptic not only tilted 60½° away from the equator but also going backwards, with the Sun going not west to east but east to west.
No wonder Pluto’s hour lines are so bizarre:
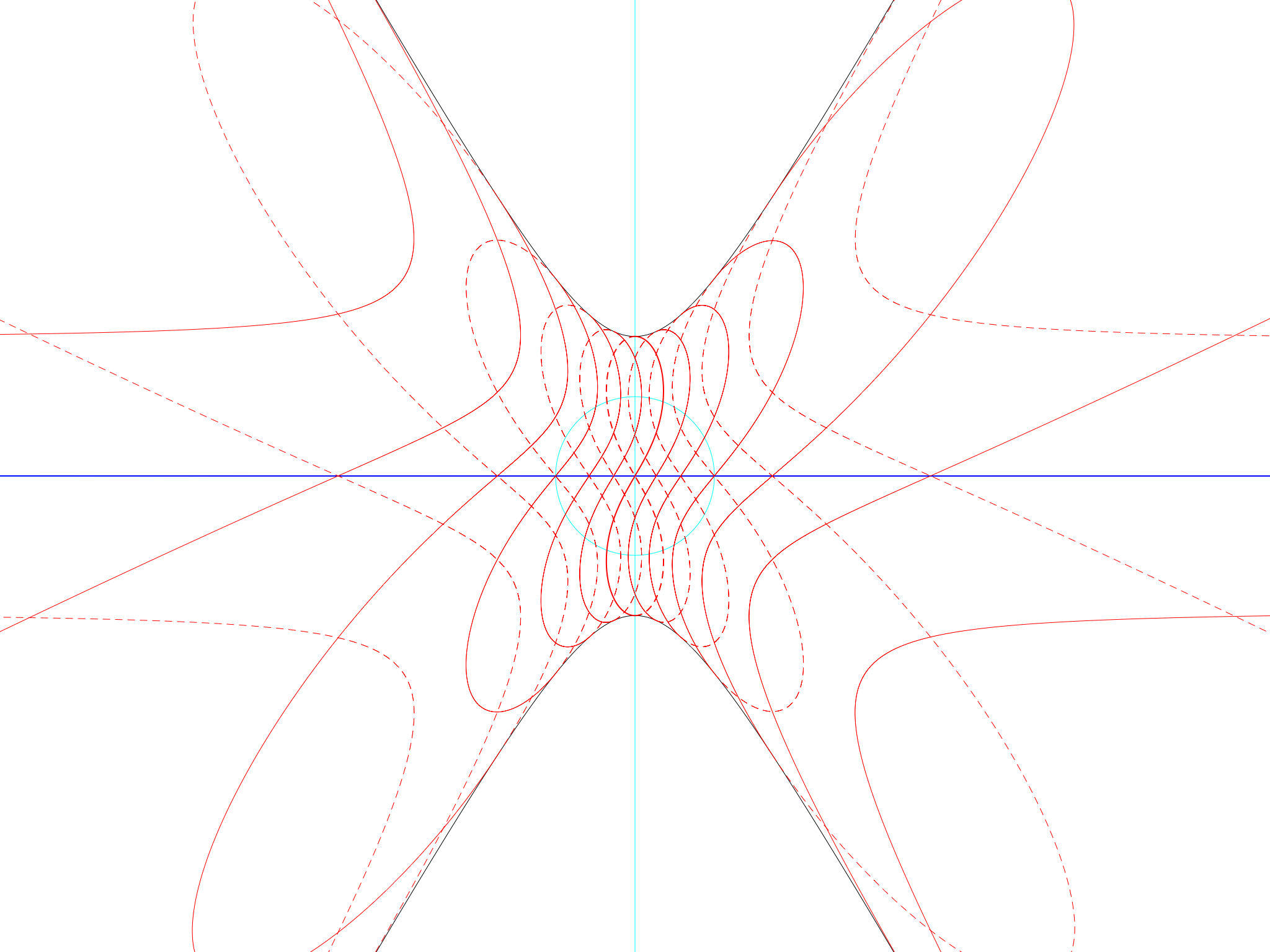 Equator on Pluto (obliquity only)
Equator on Pluto (obliquity only)The Equation of Time: eccentricity
I have just demonstrated how, if the Sun moved along the ecliptic at a constant speed, it would still be travelling east at different speeds at different times of the year.
In fact, the Sun does not move along the ecliptic at a constant speed. Its speed is nearly constant but not quite: it varies through the course of the year. This is another example of the alternating delight and frustration of astronomy. Constant speed nearly explains everything but not quite, so now we have to measure the inconstancy and find out what law it follows.
The Greeks already knew in the fourth century B.C. that the sun’s motion was not uniform. The time from the spring equinox to the summer solstice was 94½ days and the time from the summer solstice to the autumn equinox was 92½ days, whereas if the Sun were moving uniformly then those times should have been equal. The Greek astronomer Hipparchus gave the first theoretical explanation of this in the second century B.C. He calculated that the Sun must be going at its fastest in early January (the modern date for this is the 3rd of January).
What about the law that this variation follows? Hipparchus used the simplest possible model as an explanation of this phenomenon: the Sun moves uniformly in a circle but around a point that is not in the centre of the Earth. The distance between the Earth and the central point was called the eccentricity of the Sun’s orbit.
The modern explanation depends on high-precision measurements made almost two millennia later, and on Johannes Kepler’s brilliant analysis of them – brilliant, because the difference between Kepler’s theory and Hipparchus’s was so small; also brilliant, because when Kepler was working out his theory Isaac Newton had not yet been born, and gravity was something that happened on the Earth, making things fall, and not among the stars. Indeed, there was no theory of what could make planets move for ever and not stop, or indeed what was making them go round and round. When Newton finally did work out his theory of universal gravitation, it fitted Kepler’s laws of planetary motion just as a lock fits round a key. Kepler’s genius was to create the right key before the lock was even known.
Kepler worked out that the Earth does not orbit the Sun in a circle, not even in an off-centre circle, but in an ellipse. An ellipse is a sort of squashed circle but its exact properties aren’t important here. What is important is that the Earth isn’t aways at the same distance from the Sun. The distance by itself doesn’t matter – we can hardly measure it – but its consequences do matter because all orbits share an important property: the closer an orbiting body is to its parent, the faster it moves. For instance, twice as close means twice as fast. This is usually described by saying that the body “sweeps out equal areas in equal times” but I find that is a confusing description unless you draw a lot of pictures.
The Earth and the Sun are closest together on 3 January. On that day they are a bit over 3% closer than they are on 4 July, so the Earth is moving about 3% faster. Equally, if we think of the Sun moving along the ecliptic above a stationary Earth, the Sun moves 3% faster in early January than in early July.
After that, the story is the same as it was with the obliquity: a faster Sun means a longer day because the Earth needs to turn a little bit longer to catch up with it.
The total Equation of Time
The two effects – the tilt of the Earth’s axis (which produces the obliquity of the ecliptic) and the eccentricity of the Earth’s orbit – combine together. The tilt of the axis makes the clock fast twice and slow twice in the year. By itself, the tilt makes loops, but it makes symmetrical ones. The eccentricity makes the clock fast once and slow once. Over the course of the year, sometimes the two effects pull in the same direction (so the overall effect is bigger) and sometimes they pull against each other and the overall effect is quite small.
The obliquity effect is tied to the 21st of March, June, September and December, while the eccentricity effect is tied to the 3rd of January and the 4th of July.
This is why the loops are rather squashed and have such an irregular shape. They come from the combination of two effects with different rhythms. The winter loop is much wider because winter is near both 21 December (when obliquity is making the day longer) and 3 January (when the eccentricity is making the day longer), so that both effects are lengthening the day at the same time. The summer loop is such a pathetic little thing because summer is near 21 June, when obliquity is making the day longer, but also near 4 July, when eccentricity is making it shorter, so that the effects pull in opposite directions and don’t add up to much.
Here are some numbers, taking into account both effects together:
Earth’s longest day: 24 hours plus 30 seconds, on 23 December.
Earth’s shortest day: 24 hours minus 21 seconds, on 17 September.
Mean Time
Solar time is easy to define accurately: noon is noon is noon. What about clock time? How do we define that?
All we need to do is pick one moment in time and give it a name. Every other moment in time will then acquire a name as well, because all we need to do is count how many hours there are between that moment and our chosen “master moment”.
It is a question of what master moment to choose, and what name to give it. (If that sounds like deciding what time zone a country should use, that is because it really is the same thing).
One of the aims of clock time is that 12pm should be near noon. After all, we do talk about “12 noon”. We know now that 12pm can’t always be noon because the time from one noon to the next is practically never 24 hours exactly. But all the same, “12 noon” is an aim worth pursuing.
The following examples come from detailed calculations which I haven’t shown you, so don’t worry about where the numbers come from, just look at the general idea:
- If I decided to call solar noon on the 2nd of November “12 noon”, then 102 days later, on the 12th of February, noon would be at 12:30 by the clock. Over the course of the year, noon would be between 12:00 and 12:30.
- If I decided to call solar noon on the 12th of February “12 noon” then on the 2nd of November, noon would be at 11:30 by the clock, and over the course of the year, noon would be between 11:30 and 12:00.
In the first example, as you go through the year the average time of noon is about a quarter of an hour after 12pm, by the clock.
In the second example, the average time of noon is about a quarter of an hour before 12pm, by the clock.
So what about picking a definition of “12pm” that is more or less half way between these two? If we picked it carefully, we could make the average (or “mean”) time of noon over the course of the year exactly 12pm. The clock would still practically never be right, compared to the sun, but it would be as little wrong as it could be, and on average, over the course of a year, it would be neither fast or slow.
That is the definition of “mean time” and it is how Greenwich Mean Time was designed.
Now I can show you a couple of other facts about the Equation of Time. I couldn’t show them before because we didn’t yet have a definition of where clock time should start.
Clock fastest, sundial slowest: 14.24 minutes slower than the clock on 12 February.
Clock slowest, sundial fastest: 16.42 minutes faster than the clock on 2 November.
A quick glance at Mars
Mars is quite similar to the Earth, so it is interesting to see how it compares when it comes to sundials.
Here, as a reminder, is the diagram you have already seen for the Earth.
 Equator on Earth
Equator on EarthAnd here is how the same diagram would look on Mars:
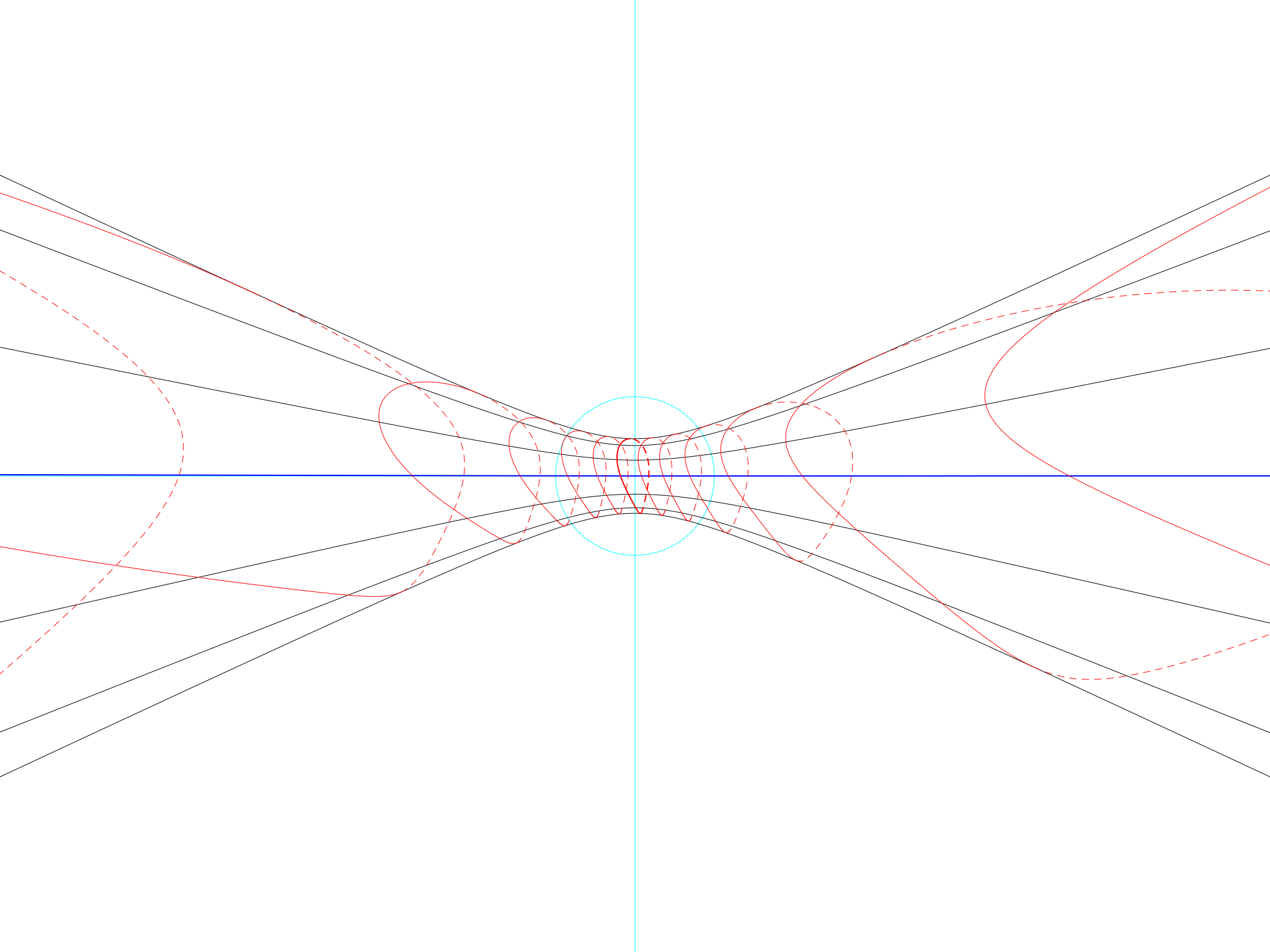 Equator on Mars
Equator on Mars
The black shadow lines are slightly more widely spread. This is because Mars’s axis is slightly more tilted than the Earth’s (25° instead of 23½°). But the real difference is in the hour lines. They are much, much fatter at the top, but the bottom half of the figure of eight, which was already squashed for the Earth, has been squashed into non-existence on Mars. The bottom loop has completely disappeared and the only shadow of its existence is that the bottom of the fat bulbous hour line is a little pointed compared to the top.
This is because Mars’s orbit is much more eccentric than the Earth’s, so the eccentricity effect is that much more powerful. (In fact, Mars was the only planet whose eccentricity was observable enough for Kepler to make his great discovery about ellipses, because only for Mars was the difference between “off-centre circle” and “ellipse” measurable by the most precise instruments of the early 17th century).
The result of all this is that the loops don’t just come towards each other, as they do on Earth: they overlap. If you look closely, you’ll see that on Mars the position of the Sun at noon at the beginning of spring is the same as the position of the Sun at 11am at the beginning of autumn. Martians will have to reconcile themselves to very inaccurate sundials or with clocks that are up to half an hour faster or slower than the Sun.
Or they may also just decide to have two curved lines engraved on a sundial: a spring line (corresponding to the solid red lines in the picture) and an autumn one (the dotted lines). Better still, they could have two interchangeable discs, one for the first half of the year and one for the second. They could mark the summer solstice with a Japanese-style ceremony of “the changing of the sundials”.
Back to Pluto
And so to Pluto. How do all these explanations and calculations work there?
Pluto is crooked, and Pluto is eccentric: much more crooked and much more eccentric than the Earth or Mars.
Pluto‘s ecliptic is tilted at 60½ degrees to its equator. As you’ve seen already, that, on its own, would make the hour lines on a sundial look like this:
 Equator on Pluto (obliquity only)
Equator on Pluto (obliquity only)It has to be said that although this is a tangle, it is a very beautiful tangle. Peering into it, one can see that the central regions, near noon, are much like the Earth’s except that they overlap more. In Pluto’s equivalent to “February” the Sun is in the same place in the sky at 12pm as it is at about 2.30pm in Pluto’s “November”.
Eccentricity
As well as Pluto’s axis being very tilted, Pluto’s orbit is very eccentric: 15 times more eccentric than the Earth’s. There isn’t a mere 3% difference between the closest and furthest distance from the Sun: Pluto, at its closest, is ⅗ as far from the Sun as it is at its furthest point. The way solar radiation works, this means that Pluto gets almost three times as much heat from the Sun when it is closest to it. The effect on its climate must be interesting, to say the least. Scientists have speculated that when Pluto is furthest away from the Sun, its whole atmosphere will freeze (and other scientists have speculated that it won’t: that is how science works).
A few numbers
To give an idea of the ways in which Pluto differs from the Earth, here are a few facts. I have made Pluto’s year seem normal to us by dividing it into 365 equal steps and giving them the same name as our own days. This isn’t a proposal for a Plutonian calendar (that would be idiotic: Pluto’s year has 10,000 days, not 365) but it gives an immediately comprehensible idea of how far we have got through its year. In the same way, when I talk about “hours” and “minutes” on Pluto, I mean 24ths and 1440ths of Pluto’s day, not ours. Again, this is to make the day seem normal without calculations.
Here are the seasons:
| Date | Pluto | Earth |
|---|---|---|
| Spring equinox | 21 March | 21 March |
| Summer solstice | 21 May | 21 June |
| Autumn equinox | 15 September | 21 September |
| Winter solstice | 16 January | 21 December |
Spring on Pluto is very short: the longest day happens a whole “month” early. Winter is very short too: the shortest day happens a “month” late. Summer and autumn are therefore extra long, to make up. This is because Pluto is closest to the Sun at the time of its Spring equinox (on its “23 March”, actually) and it is going much faster in its orbit, so it gets to the “solstice” point in the orbit that much sooner. On the way to and from the autumn equinox, Pluto is far from the Sun and orbiting much more slowly. There is an excellent picture at the Planetary Society’s web site, which explains it better than any words can. I used it repeatedly when my program was giving me results I did not believe. The program was always right, but Pluto is indeed hard to believe sometimes!
The description I’ve written of why the Earth’s day is 24 hours long still works for Pluto, but you have to re-read it carefully, and think backwards while you do it. For us, the Sun goes west to east along the ecliptic so that the faster it goes, the longer the time from noon to noon: faster Sun means longer days. On Pluto, the Sun goes from east to west along the ecliptic, so that the faster it moves, the shorter the time from noon to noon: faster Sun means shorter days. Logical, but another piece of Plutonian strangeness.
As for how accurate a sundial is, here are the numbers. Remember that the dates are Pluto “dates” and the hours are Pluto “hours”.
Pluto’s longest day: 24 hours plus 4 seconds, on 17 September.
Pluto’s shortest day: 24 hours minus 8 seconds, on 16 May.
That doesn’t sound like much, but remember that Pluto’s year is 10,000 days, not 365, so that compared to us, the differences have many more days over which to accumulate. The conclusion is:
Clock fastest, sundial slowest: 181 minutes slower than the clock on 16 December.
Clock slowest, sundial fastest: 189 minutes faster than the clock on 20 June.
Plutonians would have great difficulty with clocks. At some times of the year and at some latitudes, 12pm by the clock might be before sunrise or after sunset!
Some more pictures at last
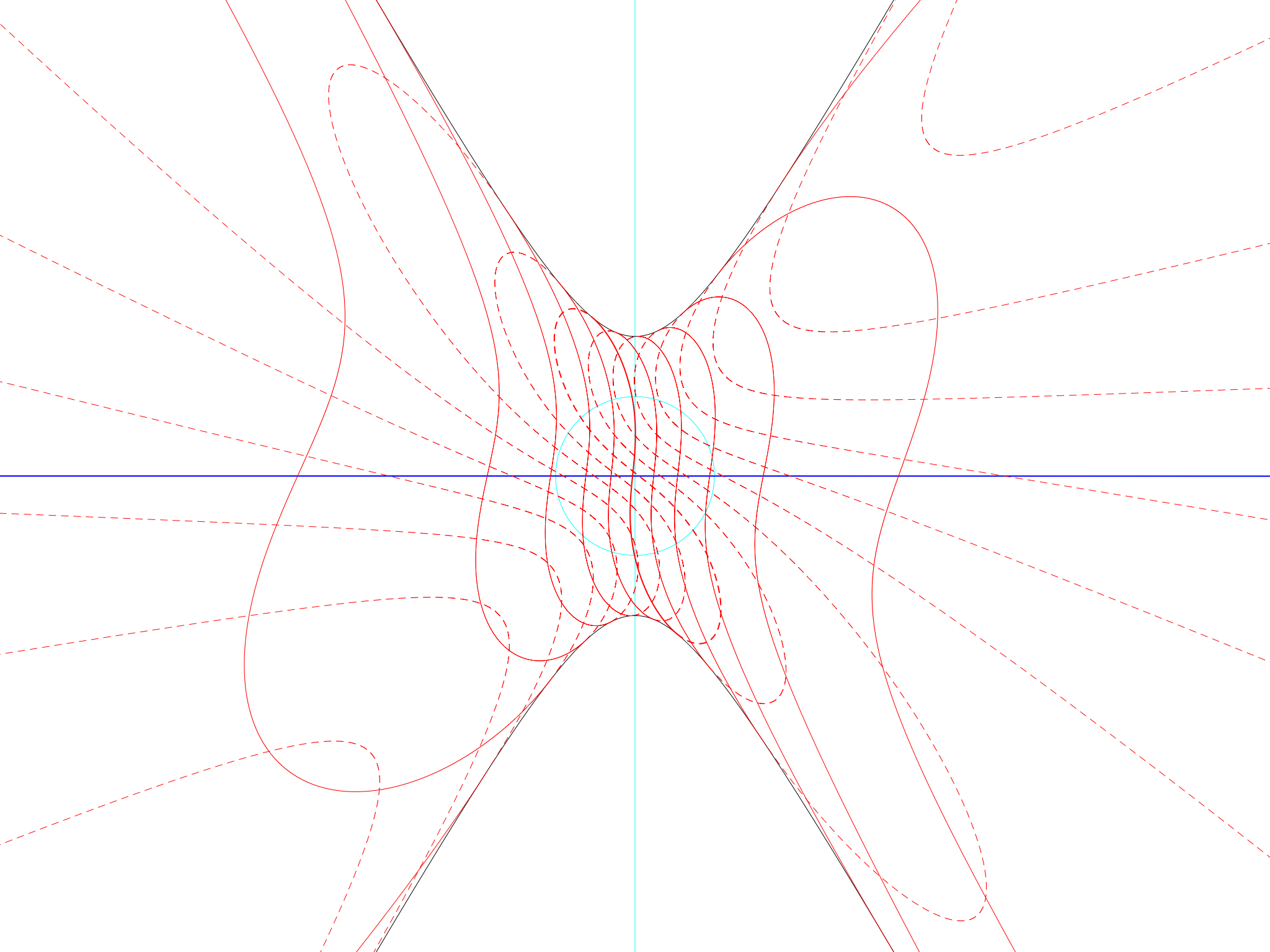 Equator on Pluto
Equator on Pluto This pattern should be not so much studied as contemplated. Like a good atlas, the thing to do is to stare at it and dream.
The middle part of the December-to-June trip from solstice to solstice (marked by the solid red lines) is fairly upright and straight. Does this mean, I ask myself in my dream, that in that period sundials and clocks will agree?
On the other hand, the dotted red lines, the June-to-December lines, are at a steep angle. But they are at the same steep angle. This is the sort of pattern I was getting when there was a bug in the program and it was getting the day length wrong. So perhaps, after some confusion at the solstices themselves, the Plutonians set their watches to lose 5 Pluto “seconds” each day in summer and autumn, and the watches will match the behaviour of the Sun.
I’m not going to try to work out the details. You don’t do that with dreams. That is not the point of them.
Here are a few more pictures for dreaming with.
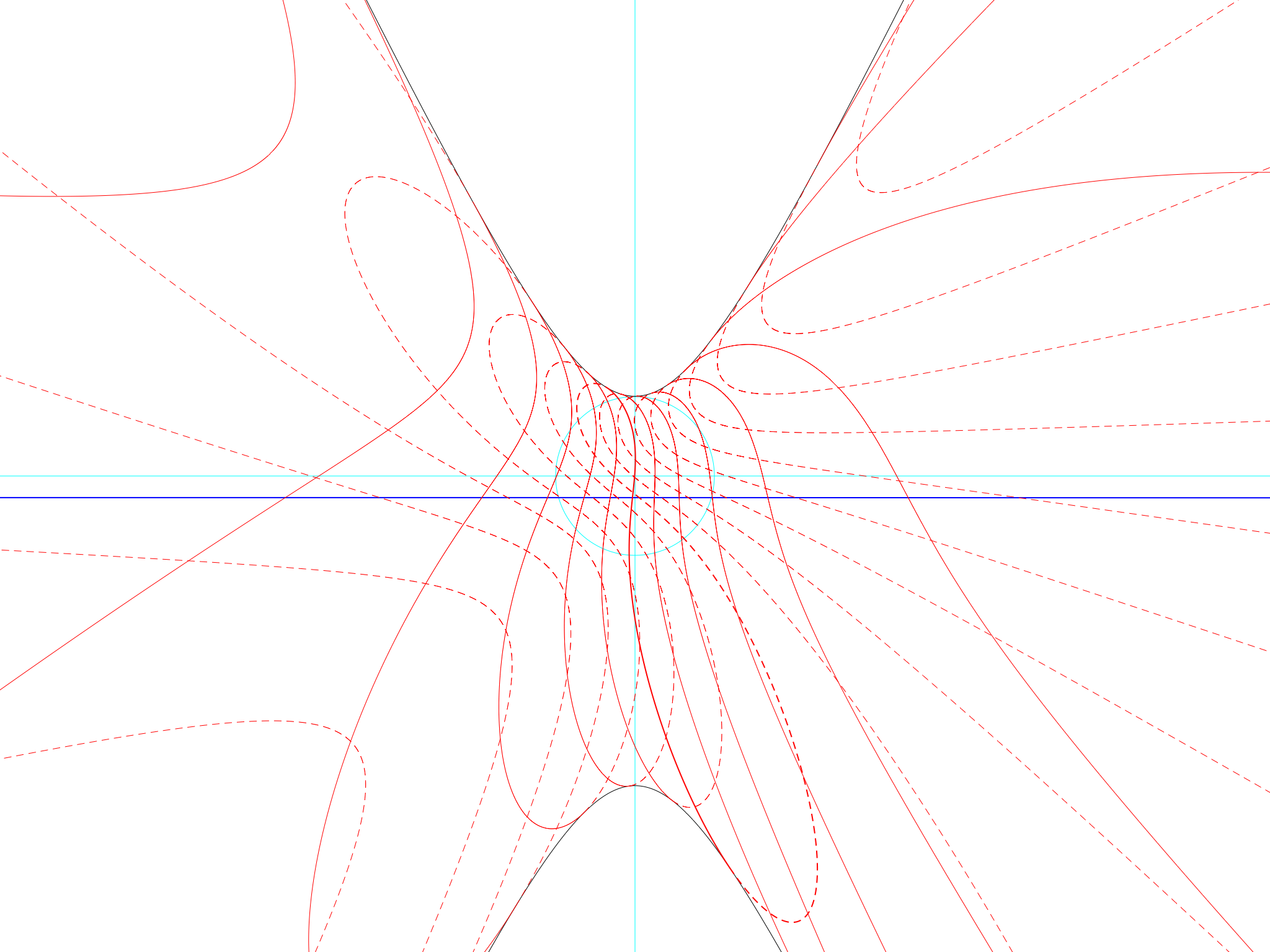 Pluto, latitude 15°S
Pluto, latitude 15°S Pluto, latitude of Greenwich
Pluto, latitude of Greenwich  Pluto, North Pole
Pluto, North Pole On to other worlds
Mercury is intellectually interesting but visually dull. It orbits the Sun every 88 days. It turns on its axis once every 58 days.
When the Earth has rotated on its axis in 23 hours 56 minutes, the Sun has got a bit ahead of where it was, and it takes about 4 minutes for the Earth to catch up. (Of course, in that time the Sun has moved a tiny bit ahead, so there is a very tiny bit of extra turning for the Earth to do and it isn’t even worth talking about separately).
The books will tell you that Mercury rotates in 58 of our days and orbits the Sun in 88 of our days.
To make it seem more like Earth, let me re-do these numbers. A “Mercurian hour” is a 24th of the time from one noon to the next. That makes a “Mercurian hour” about as long as an Earth week.
- Mercury rotates on its axis (relative to the fixed stars) in 8 “Mercurian hours”.
- Mercury orbits the Sun (or the Sun orbits Mercury, if you prefer) in 12 “Mercurian hours”.
When you lie on your back and look up at the stars, after 8 hours you are looking up towards the same star you were looking up at originally, but the Sun has moved ahead, by ⅔ of an orbit.
Wait another 5 hours 20 minutes and you will be looking up at… where the Sun was when you started trying catch up with it. But of course it has moved on again. You have to wait another 3½ hours… but the Sun (never standing still) has moved on ahead.
The net result is that you have to spend 24 “Mercurian hours” in your race with the Sun. In that time you will have passed the same star (Sirius, let’s say) three times but the Sun will only have passed it twice. To put it in different words, 24 “Mercurian hours” make 3 sidereal days or 2 solar years.
Mercury’s solar day lasts two of its years. That is already strange, but there is more to come.
Mercury: Eccentricity and heat
Having a day which lasts exactly two years means that whatever place in its orbit Mercury is now, it will be in that place at the same time every day (and also in that place 12 “Mercurian hours” later).
This also applies to the point in its orbit where Mercury is closest to the Sun (the perihelion).
Mercury’s orbit, like Pluto’s, is very eccentric, and the Sun is already huge and hot because Mercury is so close to the Sun. So at the perihelion the Sun is extremely huge and hot. The point on the equator at which the Sun is directly overhead at perihelion (the point where perihelion is at “12 noon” Mercurian time) is the hottest place on the planet.
It is so much hotter than everywhere else that astronomers have decided to use it as the planet’s “Greenwich meridian”, its definition of 0° longitude.
(Of course every point on the equator has the Sun directly overhead at some moment in the day, but only at 0° and 180° longitude does this coincide with the Sun being at its nearest and hottest).
So as well as its North Pole and its South Pole, Mercury has two “hot poles”.
Mercury: Eccentricity and time
There is one more thing. Here is the story of star days and sun days carefully split into bullet points:
- The Earth rotates from west to east under the stars at 15.04° per hour.
- So the stars are moving from east to west above the Earth at 15.04° per hour.
- The Sun is moving through the stars slowly from west to east, at 0.04° per hour.
- So the Sun is moving from east to west above the Earth, but more slowly than the stars are. Its speed is 15.04−0.04, or 15° per hour.
- The Earth’s orbit is slightly eccentric, and so on the 3rd of January the Sun is moving through the stars at a bit more than 0.04° per hour, so it is moving from east to west above our heads at a bit less than 15° per hour, so the day is about 20 seconds longer than average.
So here are the numbers with Mercury:
- Mercury rotates from west to east under the stars at 45° per “Mercurian hour”.
- So the stars are moving from east to west above Mercury at 45° per Mercurian hour.
- The Sun is moving through the stars rapidly from west to east, at 30° per Mercurian hour.
- So the Sun is moving from east to west above the Earth, but more slowly than the stars are. Its speed is 45−30, or 15° per Mercurian hour.
- Mercury’s orbit is very, very eccentric. So much so that at its perihelion, the Sun is moving from west to east through the stars very much faster: at more than 45° per Mercurian hour. This means that at perihelion, the Sun is moving from west to east (relative to the stars) faster than the stars are moving from east to west (relative to Mercury). To someone lying on the ground and looking up, the Sun will have slowed down and stopped, and started going backwards. It goes backwards for 8.1 Earth days, or just over one Mercurian hour.
- Eventually as Mercury moves further away from the Sun again (and the Sun from Mercury), the Sun’s speed through the stars reduces. It stops going backwards (west to east) and starts going forwards again.
The effect at the “hot pole”, where the Sun is directly overhead at the time of perihelion, is truly bizarre (and uncomfortable). The Sun ascends and reaches its highest point, which is noon. It goes slightly past it, then changes its mind and starts going backwards, through its highest point: noon again. Finally it makes up its mind properly and goes forward: noon yet again. The times between the three noons depend on one’s exact longitude, but at Mercury’s official 0° of longitude I have calculated that there are 5½ of our days between the first noon and the second and 8½ of them between the second noon and the third.
Unfortunately, to spoil a good story, the Sun only goes backwards by about 1° in the sky and since its diameter (viewed from Mercury) is more than that (it is 1.7°), nobody will really notice the backward movement unless he has precise instruments and a lot of courage. The Sun will just look as if it is sitting still for a couple of Mercurian hours.
Mercury: The boring news
I thought that all this should make for wonderful designs for a sundial. I put the numbers in and ran the program, and all I got was a straight line. Was it a bug?
No, it was worse than that: it was correct. Mercury is hardly tilted at all, relative to its orbit (unlike the Earth’s 23½° or Pluto’s 60½°). The Sun never deviates to north or south, but is always directly above the equator. The line of the shadow on the sundial is consequently a single, straight line.
That doesn’t stop a sundial working, of course, though it does make it look a lot less decorative. More seriously, if the Sun is in essentially the same place in the sky for up to three Mercurian hours, any hour lines you tried to draw on the sundial would be stuck together and slightly entangled around noon.
Fortunately Mercury has no atmosphere to speak of, so there is an alternative. As long as you shade your eyes with your hand, you will be able to see the stars even at midday. They go round the sky at an absolutely steady pace, once every 12 Mercurian hours. It is quite possible that Mercurians would end up telling the time by the stars rather than by the Sun.
Venus
Venus orbits the Sun in 224 days. As for its own rotation, it is the slowest-spinning body in the Solar System, languidly turning on its axis every 243 days. Astronomers love finding excuses for this languor (and insisting that the fact that Venus’s day is exactly ⅔ of an Earth year is nothing but a coincidence) – and they also love finding explanations of the fact that Venus spins backwards. The Sun, on Venus, rises in the west and sets in the east, and a solar day is worth 117 of our days (or minus 117 of our days, as some pedants prefer to say).
Unfortunately all this is of no use to the sundial maker. Not only is Venus as depressingly untilted as mercury, so that the line of the Sun’s shadow is just a boring straight line, but it is also entirely covered in clouds, so a sundial wouldn’t show shadows anyway.
The Moon
The Moon is tantalizing. It shares an orbit with the Earth but it has a different tilt and it turns on its axis only once every 27⅓ days, so the shadow patterns will be interestingly different.
The Moon is definitely the next place to try.